دوره هندسه‌خوانی(۲)

G مرکزثقل - کلاسیک

خبببببب...امروز میخایم نقطه‌ی جذابِ G رو از دید هندسه‌ی کلاسیک بررسی کنیم. دوتا جمله‌ی کلیدی زیر معمولا تو حل سوالای مربوط به G کمکمون میکنه

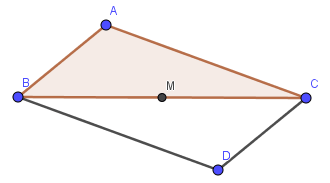
فرض کنید AM میانه‌ی نظیرِ راس A از مثلث ABC باشه در این صورت:

جمله‌ی اول :‌ G نقطه‌ای است که خطِ AM را به نسبت ۲ به ۱ تقسیم می‌کند بطوریکه AG=2GM

جمله‌ی دوم : اگر AM را به اندازه‌ی خودش امتداد دهیم تا به نقطه‌ی D برسیم، چهارضلعی ABCD متوازی‌الاضلاع است.

مثال ۱-۲

ثابت کنید مرکز ثقل مثلث ABC و مرکز ثقل مثلثی که راس‌های آن اوساط اضلاع AB و BC و AC باشد برهم منطبق‌اند.(به مثلث ایجاد شده از اوساطِ اضلاعِ مثلثِ ABC، مثلثِ میانک یا مثلثِ مکملِ ABC می‌گویند.)

حل:

D و E و F را به ترتیب اوساط اضلاعِ BC و AC و AB نامگذاری می‌کنیم. طبق تشابه مثلث‌های ABC و AEF(دوضلع و زاویه‌ی بین) EF موازی BC است. پس میانه‌ی AD از وسط EF یعنی M می‌گذرد.(شکل زیر را ببینید!) G و 'G را به ترتیب مرکز ثقل مثلث اصلی و مثلث میانک می‌گیریم که هر دو روی خط AD قرار دارد پس کافیست نشان دهیم فاصله‌ی G و 'G از نقطه‌ی D به یک اندازه است. طبق جمله‌ی اول فاصله‌ی DG یک‌سومِ AD و 'DG برابر است با دوسومِ DM و DM نصفِ AD است. پس 'DG=DG.

توضیحات شکل: AD پاره خطِ BC رو نصف میکنه و فقط پاره‌خطی رو نصف میکنه که موازی BC باشه. اگر بجای نصف کردن، خطِ AD پاره خطِ BC رو به هرنسبتی مثلا K تقسیم کنه بازم فقط و فقط خط موازیِ ‌BC رو به همین نسبت جدا می‌کنه.

شهود:

دو خط همرس در A را تصور کنید و فرض کنید B و E دو نقطه روی یکی از خطوط و نقاطِ C و F روی خط دیگر قرار دارند. چهار پاره خط AB AE AC AF ایجاد میگردد که دوتای اول روی یک خط و دوتای دوم روی خط دیگرند. اگر ضرب طول هر دوتا از پاره خط ها برابر با ضربِ طولِ دو پاره خط دیگر شود این چهار نقطه یا(چرا؟)

حالت اول: روی دوخط موازی قرار دارند

حالت دوم: روی دایره قرار دارند(BEFC محاطی است) 

حال تصور کنید E روی امتدادِ AB حرکت کند، در این صورت برای اینکه تساوی ضرب طول‌ها همچنان برقرار بماند باید F بگونه ای جابجا شود که همه‌ی EFها موازی هم باشند و در حالت اول همه‌ی EFها موازی BC هستند و در حالت دوم همه‌ی EF ها را می‌گوییم پادموازیِ BC هستند و خود EF ها موازی یکدیگر هستند و تشکیل چهارضلعی های محاطی BCFE می‌دهند.

قضییه ۱-۲

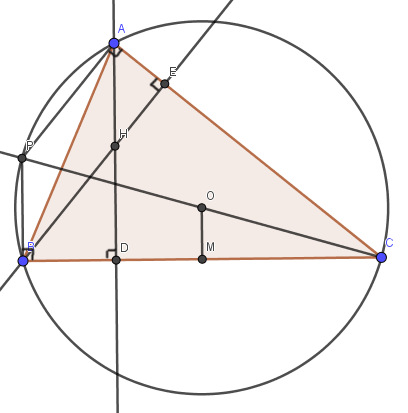
اگر H محل همرسی ارتفاع‌های مثلث ABC باشد(مرکز ارتفاعیه) و O محل همرسی عمود منصف‌های اضلاع آن مثلث باشد(مرکزِ دایره محیطی مثلث) و M وسط ضلعِ BC باشد، AH=2OM

حل:

می‌دانیم هرنقطه‌ای روی دایره، قطرِ دایره را با زاویه‌ی ۹۰ درجه می‌بیند. پس در شکل زیر زوایای PBC و PAC قائمه هستند. بنابراین PB و PA به ترتیب موازی ارتفاع‌های AD و BE هستند پس APBH متوازی‌الاضلاع است در نتیجه AH=PB=2OM(چرا؟ PB=2OM)

مثال ۲-۲

نشان دهید نقاطِ H و G و O هم‌خط(خط اویلر) هستند که H مرکز ارتفاعیه، G مرکز ثقل، O مرکز دایره‌ی محیطیِ مثلث ABC است و HG=2GO

حل:

طبق قضییه‌ی بالا  AH=2OM و طبقِ جمله‌ی اول AG=2GM و زوایای HAG و OMG برابر هستند پس مثلث‌های AHG و MOG متشابه هستند(ض‌ز‌ض) در نتیجه زوایای HGA و OGM برابر هستند. درنتیجه نقاطِ H و G و O روی یک خط قرار دارند و HG=2GO

مثال ۳-۲

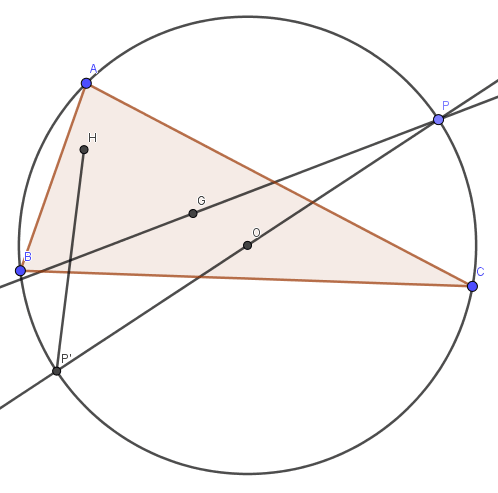
فرض کنید P نقطه‌ی دلخواهی روی دایره‌ی محیطی مثلث ABC باشد و 'P روبرو قطریِ P باشد('PP قطر دایره است). نشان دهید PG از وسطِ 'HP می‌گذرد که H و G به ترتیب مرکز ارتفاعیه‌ و مرکز ثقل مثلث ABC است.

حل:

O وسطِ 'PP پس HO میانه‌ی وارد بر ضلع 'PP از مثلثِ 'HPP که از G می‌گذرد. از مثال قبل می‌دانیم HG=2GO و HO میانه است پس طبق جمله‌ی اول G مرکز ثقل مثلث 'HPP هم هست. بنابراین PG از وسط 'HP عبور می‌کند.

لِم ۱-۲

(قانون کسینوس‌ها) در مثلث ABC طول اضلاع  a , b , c  هستند. نشان دهید :

حل:

ارتفاع AD را رسم می‌کنیم، طبق قضییه‌ی فیثاغورث می‌توان نوشت

مثال ۴-۲

طولِ میانه‌ی نظیر راسِ A را بر حسب اضلاعِ مثلث a , b , c حساب کنید.

حل:

اگر میانه‌ی AM را به اندازه‌ی خودش امتداد دهیم تا به نقطه‌ی D برسیم، ABCD متوازی‌الاضلاع است(جمله‌ی دوم). بنابراین طبق قانون کسینوس‌ها در مثلث ADC و استفاده از قانون کسینوس‌ها در مثلث ABC برای بدست آوردن کسینوس زاویه‌ی A می‌توان نوشت:

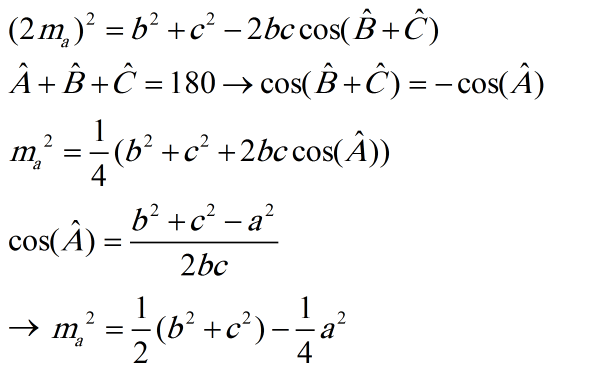
که در حالتِ خاصِ مثلث قائمه الزاویه با جمله‌ی میانه‌ی وارد بر وتر نصف وتر است سازگاری دارد.

مثال ۵-۲

خطی به موازات میانه‌ی AM از مثلث ABC رسم می‌کنیم تا خطوطِ BC و AB و AC را به ترتیب در نقاط D و E و F قطع کند. اوساطِ BE و CF به ترتیب K و 'K می‌نامیم. اگر DK و 'DK را به اندازه‌ی خود از سمتِ K و 'K امتداد دهیم تا نقاطِ X و Y حاصل شود، نشان دهید A وسطِ پاره‌خطِ XY است.

حل:

کافیست نشان دهیم 'AKDK متوازی‌الاضلاع است(چرا؟)

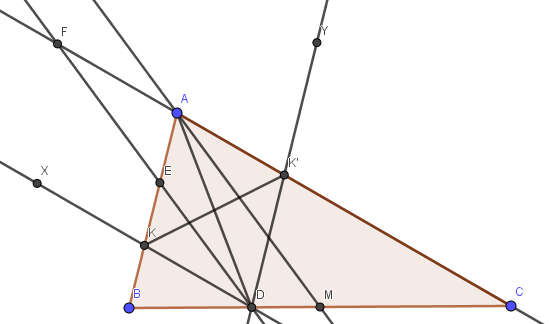
AM را به اندازه‌ی خودش امتداد می‌دهیم تا 'A ایجاد شود. طبق جمله‌ی دوم XBDE و ABA'C متوازی‌الاضلاع هستند. امتداد ED خطِ 'BA را در T قطع می‌کند. از T موازی BC خطی رسم می‌کنیم تا XB را در I قطع کند.(شکل زیر) ET موازی 'AA است پس ED=DT و می‌دانیم XBDE متوازی‌الاضلاع است پس XB=DT و این دوخط موازی هستند پس XBTD متوازی الاضلاع است(چرا؟). پس DK موازی BT و در نتیجه موازی AC است. به همین شکل 'DK موازی AB است پس چهارضلعیِ 'AKDK متوازی‌الاضلاع است.

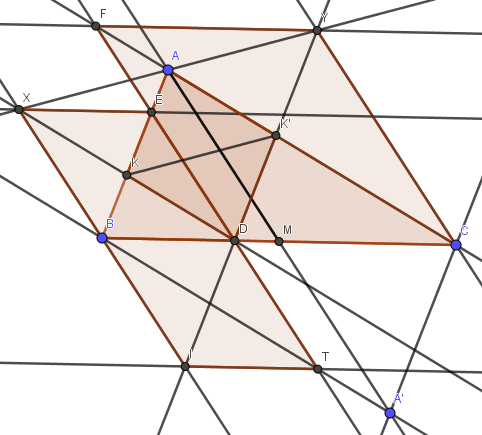
ادامه‌ دارد....